Descriptive Statements:
- Apply trigonometric functions to solve problems involving distance and angles.
- Apply trigonometric functions to solve problems involving the unit circle.
- Manipulate trigonometric expressions and equations using techniques such as trigonometric identities.
- Analyze the relationship between a trigonometric function and its graph.
- Use trigonometric functions to model periodic relationships.
Sample Item:
Which of the following are the solutions to
2 sin2 θ = cos θ + 1 for 0 < θ ≤ 2π2 sine squared theta equals cosine theta plus 1 for 0 is less than theta is less than or equal to 2pi?
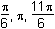
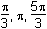
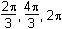
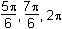
Correct Response and Explanation (Show Correct ResponseHide Correct Response)
B. This question requires the examinee to manipulate trigonometric expressions and equations using techniques such as trigonometric identities. Since sin2 θ = 1 – cos2 θ, 2 sin2 θ = cos θ + 1 ⇒ 2(1 – cos2 θ) = cos θ + 1 ⇒ 2 cos2 θ + cos θ –1 = 0 ⇒ (2 cos θ – 1)(cos θ + 1) = 0 ⇒ cos θ = 1/2 or cos θ = –1. Thus for 0 < θ ≤ 2π, θ = π/3, 5π/3, or πsine squared theta equals 1 minus cosine squared theta, 2 sine squared theta equals cosine theta plus 1 which becomes 2 times the quantity 1 minus cosine squared theta equals cosine theta plus 1 which becomes 2 cosine squared theta plus cosine theta negative 1 equals 0 which becomes the quantity 2 cosine theta minus 1 times the quantity cosine theta plus 1 equals 0 which becomes cos theta equals 1 half or cosine theta equals negative 1. Thus for 0 is less than theta is less than or equal to 2pi, theta equals pi over 3, 5pi over 3, or pi.
Descriptive Statements:
- Evaluate limits.
- Demonstrate knowledge of continuity.
- Analyze the derivative as the slope of a tangent line and as the limit of the difference quotient.
- Calculate the derivatives of functions (e.g., polynomial, exponential, logarithmic).
- Apply differentiation to analyze the graphs of functions.
- Apply differentiation to solve real-world problems involving rates of change and optimization.
Sample Item:
If f(x) = 3x4 – 8x2 + 6, what is the value of 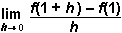 f of x equals 3x to the fourth minus 8x squared plus 6, what is the value of the limit as h approaches 0 of f of the quantity 1 plus h minus f of 1 all over h?
f of x equals 3x to the fourth minus 8x squared plus 6, what is the value of the limit as h approaches 0 of f of the quantity 1 plus h minus f of 1 all over h?
- –4negative 4
- –1negative 1
- 1
- 4
Correct Response and Explanation (Show Correct ResponseHide Correct Response)
A. This question requires the examinee to analyze the derivative as the slope of a tangent line and as the limit of the difference quotient. The limit expression is equivalent to the derivative f'(1)f of 1. Since it is much easier to evaluate the derivative of a polynomial, this is preferred over evaluating the limit expression. f'(x)= 12x3 – 16x, so f'(1) = 12 – 16 = –4.f of x equals 12x cubed minus 16x, so f of 1 equals 12 minus 16 equals negative 4
Descriptive Statements:
- Analyze the integral as the area under a curve and as the limit of the Riemann sum.
- Calculate the integrals of functions (e.g., polynomial, exponential, logarithmic).
- Apply integration to analyze the graphs of functions.
- Apply integration to solve real-world problems.
Sample Item:
A sum of $20002000 dollars is invested in a savings account. The amount of money in the account in dollars after t years is given by the equation A = 2000e0.05tA equals 2000e to the 0.05t. What is the approximate average value of the account over the first two years?
- $21032103 dollars
- $21052105 dollars
- $22062206 dollars
- $22102210 dollars
Correct Response and Explanation (Show Correct ResponseHide Correct Response)
A. This question requires the examinee to apply integration to solve real-world problems. The average value of a continuous function f(x) over an interval [a, b] is 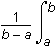 f(x)dxf of x over an interval from a to b is 1 over b minus a times the integral from a to b of f of x dx. Since the independent variable t represents the number of years, the average daily balance over 2 years will be 1/21 half of the integral of the function evaluated from 0 to 2:
f(x)dxf of x over an interval from a to b is 1 over b minus a times the integral from a to b of f of x dx. Since the independent variable t represents the number of years, the average daily balance over 2 years will be 1/21 half of the integral of the function evaluated from 0 to 2: 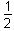
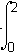 2000e0.05tdt =
2000e0.05tdt = 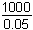 (e0.1 – 1) ≈ 21031 half the integral from 0 to 2 of 2000 e to the 0.05t dt equals 1000 over 0.05 times e to the 0.1 minus 1, which is apporximately equal to 2103.
(e0.1 – 1) ≈ 21031 half the integral from 0 to 2 of 2000 e to the 0.05t dt equals 1000 over 0.05 times e to the 0.1 minus 1, which is apporximately equal to 2103.

