Descriptive Statements:
- Identify an appropriate problem-solving strategy for a particular problem.
- Analyze the use of estimation in a variety of situations (e.g., rounding, area, plausibility).
- Solve mathematical and real-world problems involving integers, fractions, decimals, and percents.
- Solve mathematical and real-world problems involving ratios, proportions, and average rates of change.
Sample Item:
In four half-cup samples of a cereal containing dried cranberries, the numbers of cranberries were 17, 22, 22, and 18. Nutrition information on a box of this cereal defines the serving size as 1
cup or 53 grams. If a box contains 405 grams, which of the following is the best estimate of the number of cranberries in one box of this cereal?
- less than 300
- between 300 and 325
- between 326 and 350
- more than 350
Correct Response and Explanation (Show Correct ResponseHide Correct Response)
B. This question requires the examinee to analyze the use of estimation in a variety of situations (e.g., rounding, area, plausibility). There are approximately 20 cranberries per 1/21 half cup, or 40 cranberries per cup. The number of cups in a box is 405 ÷ 53405 divided by 53, which is approximately equal to 400 ÷ 50 = 8400 divided by 50 equals 8 (rounding both the numerator and denominator down minimizes the error). Thus the approximate number of cranberries in a box of this cereal is 8 × 40 = 3208 times 40 equals 320, which is within the interval of response B.
Descriptive Statements:
- Translate between representations (e.g., graphic, verbal, symbolic).
- Recognize connections between mathematical concepts.
- Analyze inductive and deductive reasoning.
- Apply principles of logic to solve problems.
- Demonstrate knowledge of the historical development of major mathematical concepts, including contributions from various groups.
Sample Item:
Given statements p and q, which of the following
is the truth table for the compound statement p ↔
(q ∨ ~p)p if and only if q or not p?
| p |
q |
p ↔
(q ∨ ~p)p if and only if q or not p |
| T |
T |
T |
| T |
F |
F |
| F |
T |
F |
| F |
F |
F |
| p |
q |
p ↔
(q ∨ ~p)p if and only if q or not p |
| T |
T |
T |
| T |
F |
F |
| F |
T |
T |
| F |
F |
F |
| p |
q |
p ↔
(q ∨ ~p)p if and only if q or not p |
| T |
T |
T |
| T |
F |
F |
| F |
T |
T |
| F |
F |
T |
| p |
q |
p ↔
(q ∨ ~p)p if and only if q or not p |
| T |
T |
T |
| T |
F |
F |
| F |
T |
F |
| F |
F |
T |
Correct Response and Explanation (Show Correct ResponseHide Correct Response)
A. This question requires the examinee to apply principles
of logic to solve problems. First a truth value column for ~pnot p is
computed as F, F, T, T (in vertical order). Then this column is
used to compute truth values for the statement q ∨ ~pq or not p: T, F, T, T.
Finally, this result is used to compute truth values for the full
expression p ↔
(q ∨ ~p)p if and only if q or not p: T, F, F, F.
Descriptive Statements:
- Analyze the group structure of the real numbers.
- Use complex numbers and their operations.
- Analyze the properties of numbers and operations.
- Apply the principles of basic number theory (e.g., prime factorization, greatest common factor, least common multiple).
Sample Item:
If p and q are prime numbers and 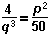 4 over q cubed equals p squared over 50 what
is the value of (p + q)left parenthesis p plus q right parenthesis?
4 over q cubed equals p squared over 50 what
is the value of (p + q)left parenthesis p plus q right parenthesis?
- 5
- 7
- 8
- 9
Correct Response and Explanation (Show Correct ResponseHide Correct Response)
B. This question requires the examinee to apply the
principles of basic number theory (e.g., prime factorization,
greatest common factor, least common multiple). The variables can
be isolated by multiplying both sides of the equation by 50q350q cubed,
which yields 200 = p2q3200 = p squared q cubed. If
p and q are both prime, then p2q3p squared q cubed
is the prime factorization of 200. Since 200 = 25 × 8 = 52 ×
23200 equals 25 times 8 equals 5 squared times
2 cubed, and 5 and 2 are both primes, p must be 5 and q must be 2, so p + q = 5 + 2 = 7p plus q equals 5 plus 2 equals 7.

