Descriptive Statements:
- Analyze the use of various units and unit conversions within the customary and metric systems.
- Apply the concepts of similarity, scale factors, and proportional reasoning to solve measurement problems.
- Analyze precision, error, and rounding in measurements and computed quantities.
- Apply the concepts of perimeter, circumference, area, surface area, and volume to solve real-world problems.
Sample Item:
Descriptive Statements:
- Demonstrate knowledge of axiomatic systems and of the axioms of non-Euclidean geometries.
- Use the properties of polygons and circles to solve problems.
- Apply the Pythagorean theorem and its converse.
- Analyze formal and informal geometric proofs, including the use of similarity and congruence.
- Use nets and cross sections to analyze three-dimensional figures.
Sample Item:
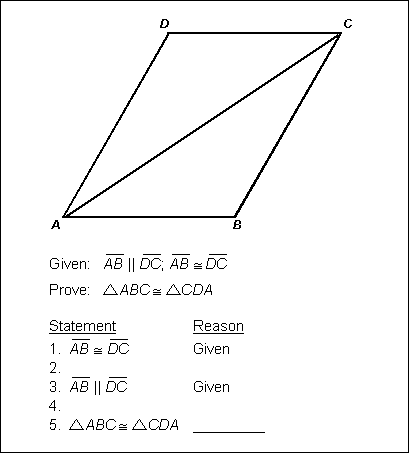
The figure is a parallelogram, ABCD. The angles at A and C are acute, and a diagonal is drawn from A to C. The proof reads as follows.
Given: Line segment AB is parallel to line segment DC, line segment A B is congruent to line segment DC.
Prove: Triangle ABC is congruent to triangle CDA.
Statement 1. Line segment AB is congruent to line segment DC. Reason, Given.
Statement 2. Blank. Reason, blank.
Statement 3. Line segment AB is parallel to line segment DC. Reason, Given.
Statement 4. Blank. Reason, blank.
Statement 5. Triangle ABC is congruent to triangle CDA. Reason, blank.
In the proof above, steps 2 and 4 are missing. Which of the following reasons justifies step 5?
- AAS
- ASA
- SAS
- SSS
Correct Response and Explanation (Show Correct ResponseHide Correct Response)
C. This question requires the examinee to analyze formal and informal geometric proofs, including the use of similarity and congruence. The side-angle-side (SAS) theorem can be used to show that ΔABCtriangle ABC and ΔCDAtriangle CDA are congruent if each has two sides and an included angle that are congruent with two sides and an included angle of the other. In the diagram AB and DCline segment AB and line segment DC are given as congruent, and the missing statement 2 is that AC is congruent to itself by the reflexive property of equality. The included angles ∠BAC and ∠DCAangle BAC and angle DCA are congruent because they are alternate interior angles constructed by the transversal ACline segment AC that crosses the parallel line segments AB and DCline segment AB and line segment DC. Thus ΔABC and ΔCDAtriangle ABC and triangle CDA meet the requirements for using SAS to prove congruence.
Descriptive Statements:
- Analyze two- and three-dimensional figures using coordinate systems.
- Apply concepts of distance, midpoint, and slope to classify figures and solve problems in the coordinate plane.
- Analyze conic sections.
- Determine the effects of geometric transformations on the graph of a function or relation.
- Analyze transformations and symmetries of figures in the coordinate plane.
Sample Item:
The vertices of triangle ABC are A(–5, 3), B(2, 2), and C(–1, –5)A left parenthesis negative 5, 3 right parenthesis, B left parenthesis 2, 2 right parenthesis, and C left parenthesis negative 1, negative 5 right parenthesis. Which of the following is the length of the median from vertex B to side AC?
- 4
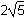 2 times the square root of 5
2 times the square root of 5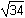 the square root of 34
the square root of 34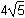 4 times the square root of 5
4 times the square root of 5
Correct Response and Explanation (Show Correct ResponseHide Correct Response)
C. This question requires the examinee to apply concepts of distance, midpoint,
and slope to classify figures and solve problems in the coordinate plane. The midpoint of side AC where its median intersects is computed as 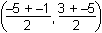 = (–3, –1)left parenthesis negative the quantity 5 plus negative 1 over 2, the quantity 3 plus negative 5 over 2 right parenthesis equals left parenthesis negative 3, negative 1 right parenthesis. The distance from B(2, 2) to (–3, –1)B left parenthesis 2, 2 right parenthesis to left parenthesis negative 3, negative 1 right parenthesis is computed as d =
= (–3, –1)left parenthesis negative the quantity 5 plus negative 1 over 2, the quantity 3 plus negative 5 over 2 right parenthesis equals left parenthesis negative 3, negative 1 right parenthesis. The distance from B(2, 2) to (–3, –1)B left parenthesis 2, 2 right parenthesis to left parenthesis negative 3, negative 1 right parenthesis is computed as d = 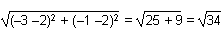 .d equals the square root of the quantity open paren negative 3 negative 2 close paren the quantity squared plus open paren negative 1 negative 2 close paren the quantity squared equals the square root of the quantity 25 plus 9 equals the square root of 34.
.d equals the square root of the quantity open paren negative 3 negative 2 close paren the quantity squared plus open paren negative 1 negative 2 close paren the quantity squared equals the square root of the quantity 25 plus 9 equals the square root of 34.

