Descriptive Statements:
- Demonstrate knowledge of relations and functions and their applications.
- Perform operations with functions, including compositions and inverses.
- Analyze characteristics of functions.
- Interpret different representations of functions.
Sample Item:
Which of the following equations represents the inverse of y = 6x − 4/1 + 3xy equals the quantity 6x minus 4 over the quantity 1 plus 3x?
- y = x − 4/3x + 6y equals the quantity x minus 4 over the quantity 3x plus 6
- y = x + 4/6 − 3xy equals the quantity x pluss 4 over the quantity 6 minus 3x
- y = 1 + 3x/6x − 4y equals the quantity 1 plus 3x over the quantity 6x minus 4
- y = 1 − 3x/6x + 4y equals the quantity 1 minus 3xover the quantity 6x plus 4
Correct Response and Explanation (Show Correct ResponseHide Correct Response)
B. This question requires the examinee to perform operations with functions, including compositions and inverses. To find the inverse of a function of the form y = f(x)y = f of x, the original equation is rearranged by solving it for x
as a function of y: y = 6x − 4/1 + 3x ⇒ y(1 + 3x) = 6x − 4 ⇒ y + 3xy = 6x − 4 ⇒ y + 4 = 6x − 3xy ⇒ y + 4 = x(6 − 3y) ⇒ x = y + 4/6 − 3yy equals the quantity 6x minus 4 over the quantity 1 plus 3x which becomes y left parenthesis 1 plus 3x right parenthesis equals 6x minus 4 which becomes y plus 3xy equals 6x minus 4 which becomes y plus 4 equals 6x minus 3xy which becomes y plus 4 equals x left parenthesis 6 minus 3y right parenthesis which becomes x equals y plus 4 over the quantity 6 minus 3y. Exchanging the variables x and y results in the inverse function f–1, y = x + 4/6 − 3xf superscript negative 1, y equals the quantity x + 4 over the quantity 6 minus 3x.
Descriptive Statements:
- Analyze the relationship between a linear, quadratic, or higher-order polynomial function and its graph.
- Solve linear and quadratic equations and inequalities using a variety of methods.
- Solve systems of linear equations or inequalities using a variety of methods.
- Solve higher-order polynomial equations and inequalities in one and two variables.
- Analyze the characteristics of linear, quadratic, and higher-order polynomial equations.
- Analyze real-world problems involving linear, quadratic, and higher-order polynomial functions.
Sample Item:
| blank | Order 1 | Order 2 | Order 3 |
|---|
| soft drink | 4 | 6 | 3 |
| large pizza | 1 | 2 | 1 |
| garlic bread | 1 | 1 | 0 |
| Total Cost | $19.6219 dollars and 62 cents | $34.9534 dollars and 95 cents | $16.5016 dollars and 50 cents |
Given the table of orders and total costs above, and that there is a solution to the problem, which of the following matrix equations could be used to find d, p, and g, the individual prices for a soft drink, a large pizza, and garlic bread respectively?
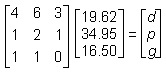
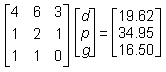
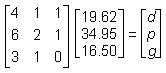
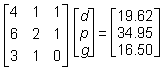
Correct Response and Explanation (Show Correct ResponseHide Correct Response)
D. This question requires the examinee to solve systems of linear equations or inequalities using a variety of methods. The system of linear equations can be solved using matrices. Each order can be expressed as an equation, with all three equations written with the variables in the same sequence. The first order is represented by the equation 4d + p + g = 19.624d plus p plus g equals 19.62, the second order by 6d + 2p + g = 34.956d plus 2p plus g equals 34.95, and the
third order by 3d + p = 16.503d plus p equals 16.50. The rows of the left-hand matrix contain the coefficients of d, p, and g for each equation: (4 1 1), (6 2 1), and (3 1 0)left parenthesis 4 1 1 right parenthesis, left parenthesis 6 2 1 right parenthesis, and left parenthesis 3 1 0 right parenthesis. The middle matrix contains the variables, d, p, g. The right-hand matrix vertically arranges the constants of the equations.
Descriptive Statements:
- Apply the laws of exponents and logarithms.
- Analyze the relationship between exponential and logarithmic functions.
- Analyze exponential and logarithmic functions and their graphs.
- Analyze real-world problems involving exponential and logarithmic functions.
Sample Item:
Which of the following is equivalent to the equation 3 log10 x − 2 log10 y = 173 log subscript 10 x minus 2 log subscript 10 y equals 17?
- 3x − 2y = 10173x minus 2y equals 10 to the power of 17
- x3 − y2 = 1017x cubed minus y squared equals 10 to the power of 17
-
x3/y2 = 1017x cubed over y squared equals 10 to the power of 17
-
3x/2y = 10173x over 2y equals 10 to the power of 17
Correct Response and Explanation (Show Correct ResponseHide Correct Response)
C. This question requires the examinee to apply the laws of exponents and logarithms.
Nloga M = loga MN ⇒ 3log10 x = log10 x3 and 2log10 y = log10 y2Nlog subscript a M equals log subscript a M superscript N which becomes 3log subscript 10 x equals log subscript 10 x cubed and 2log subscript 10 y equals log subscript 10 y squared.
Loga M − loga N ⇒ loga M/N ⇒ log10 x3 − log10 y2 = log10 x3/y2Log subscript a M minus log subscript a N which becomes log subscript a M over N which becomes log subscript 10 x cubed minus log subscript 10 y squared equals log subscript 10 x cubed over y squared.
Since loga M = N is equivalent to aN = M, then log10 x3/y2 = 17 is equivalent to 1017 = x3/y2log subscript a M equals N is equivalent to a superscript N equals M, then log subscript 10 x cubed over y squared equals 17 is equivalent to 10 to the power of 17 equals x cubed over y squared.
Descriptive Statements:
- Manipulate rational, radical, and absolute value expressions, equations, and inequalities.
- Analyze the relationship between a rational, radical, absolute value, or piece-wise defined function and its graph.
- Analyze rational, radical, absolute value, and piece-wise defined functions in terms of domain, range, and asymptotes.
- Analyze real-world problems involving rational, radical, absolute value, and piece-wise defined functions.
Sample Item:

