Recommendation for individuals using a screenreader: please set your punctuation settings to "most."
Descriptive Statements:
- Analyze the use of various units and unit conversions within the customary and metric systems.
- Calculate or estimate measures of lengths, areas, and volumes.
- Apply the concepts of similarity, scale factors, and proportional reasoning to solve indirect measurement problems.
- Analyze precision, accuracy, and rounding in measurements and computed quantities.
Sample Item:
A car is traveling at a speed of 100 kilometers per hour.
What is its approximate speed in meters per second?
- 28 meters per second
- 36 meters per second
- 280 meters per second
- 360 meters per second
Correct Response and Explanation (Show Correct ResponseHide Correct Response)
A. This question requires the examinee to analyze the use of various units
and unit conversions within the customary and metric systems. Both units in the given quantity must be
converted: kilometers to meters and hours to seconds.
100 kilometers/1 hour • 1000 meters/1 kilometer • 1 hour/3600 seconds = 27.8meters/second ≈ 28meters/second100 kilometers over 1 hour times 1000 meters over 1 kilometer times 1 hour over 3600 seconds equals 27.8 meters over second which approximately equals 28 meters over second
Descriptive Statements:
- Analyze properties of points, lines, planes, and angles.
- Use the properties of triangles, quadrilaterals, and other polygons and circles to solve problems.
- Apply principles of similarity and congruence.
- Apply the Pythagorean theorem and its converse.
- Use nets, cross sections, and projections to analyze three-dimensional figures.
- Analyze geometric arguments using deductive reasoning.
Sample Item:
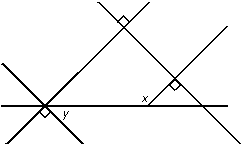
One is horizontal. Four other lines intersect the horizontal line at an unspecified angle that appears to be about 45�. The first line passes through the horizontal line near the left side of the diagram, slanted from upper left to lower right, at point y. The second line passes through point y from lower left to upper right at a right angle to the first line. The third line intersects the second line at a right angle near the top of the diagram. The third line continues toward the lower right, passing through the horizontal line near the right side of the diagram. The fourth line starts at point x on the horizontal line and goes up toward the upper right corner of the diagram, passing through the third line at a right angle.
Five lines intersect as shown. If x and y are angle measures in degrees, which of the following
equations relates y to x in the diagram above?
- y = 1/3xy equals 1 third x
- y = x − 90y equals x minus 90
- y = 1/2xy equals 1 half x
- y = 180 − xy equals 180 minus x
Correct Response and Explanation (Show Correct ResponseHide Correct Response)
B. This question requires the examinee to analyze properties of points, lines,
planes, and angles. If two lines are both perpendicular to the same transversal, the two lines are parallel.
Thus there are two pairs of parallel lines in the figure. By the alternate interior angle theorem, x = y + 90°x equals y plus 90 degrees and y = x − 90°y equals x minus 90 degrees.
Descriptive Statements:
- Analyze two- and three-dimensional figures using coordinate systems.
- Connect algebra and geometry by applying concepts of distance, midpoint, and slope to classify figures and solve problems in the coordinate plane.
- Analyze transformations of figures in the coordinate plane.
- Analyze figures in terms of symmetry, and tessellations of the plane.
Sample Item:
The end points of one diagonal of a parallelogram are (1, 3) and (1, –3)(1, negative 3). The end points of its other diagonal are (3, 1) and (–1, –1)(negative 1, negative 1). What is the perimeter of the parallelogram?
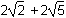 2 square root of 2 plus 2 square root of 5
2 square root of 2 plus 2 square root of 5- 10
- 20
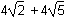 4 square root of 2 plus 4 square root of 5
4 square root of 2 plus 4 square root of 5
Correct Response and Explanation (Show Correct ResponseHide Correct Response)
D. This question requires the examinee to connect algebra and geometry by
applying concepts of distance, midpoint, and slope to classify figures and solve problems in the coordinate plane. Use points (1, 3) and (3, 1), then points (3, 1) and (1, –3),(1, negative 3), and the distance formula to find the length of two different sides of the parallelogram: 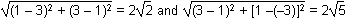 the square root of the quantity squared 1 minus 3 plus the quantity squared 3 minus 1 equals 2 square root of 2 and the square root of the quantity squared 3 minus 1 plus left bracket 1 minus left parentheis negative 3 right parenthesis right bracket squared equals 2 square root of 5. There are two of each of these sides, thus the perimeter of the parallelogram is
the square root of the quantity squared 1 minus 3 plus the quantity squared 3 minus 1 equals 2 square root of 2 and the square root of the quantity squared 3 minus 1 plus left bracket 1 minus left parentheis negative 3 right parenthesis right bracket squared equals 2 square root of 5. There are two of each of these sides, thus the perimeter of the parallelogram is 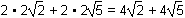 2 times 2 square root of 2 plus 2 times 2 squre root of 5 equals 4 square root of 2 plus 4 square root of 5.
2 times 2 square root of 2 plus 2 times 2 squre root of 5 equals 4 square root of 2 plus 4 square root of 5.

