Recommendation for individuals using a screenreader: please set your punctuation settings to "most."
Descriptive Statements:
- Analyze the relationships between the subsets of the real numbers.
- Analyze the role of place value in any number system.
- Analyze the use of estimation in a variety of situations.
- Translate between different representations of numbers.
- Apply number-theory concepts (e.g., divisibility rules, prime factorization, greatest common factors) in problem-solving situations.
Sample Item:
In the base-2 number system, the sum of 101 and 1011 is:
- 1000
- 1112
- 2000
- 10000
Correct Response and Explanation (Show Correct ResponseHide Correct Response)
D. This question requires the examinee to analyze the role of place value in any number system. Align addends 101 and 1011
such that place values are in the appropriate columns. Add the two digits in the right column, 1 + 1 = 21 plus 1 equals 2. The 2 is regrouped as
equaling 1 × 21 + 0 × 201 times 2 superscript 1 plus 0 times 2 superscript 0 with the 1 carried to the next column (Table 1). Continue
the process until complete (Table 2), regrouping as needed, yielding the sum 10000.
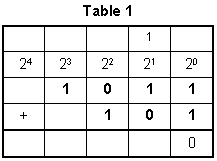
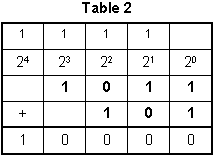
Table 1
| blank |
blank |
blank |
1 |
blank |
| 242 superscript 4 |
232 superscript 3 |
222 superscript 2 |
212 superscript 1 |
202 superscript 0 |
| blank |
1 |
0 |
1 |
1 |
| + |
blank |
1 |
0 |
1 |
| blank |
blank |
blank |
blank |
0 |
Table 2
| 1 |
1 |
1 |
1 |
blank |
| 242 superscript 4 |
232 superscript 3 |
222 superscript 2 |
212 superscript 1 |
202 superscript 0 |
| blank |
1 |
0 |
1 |
1 |
| + |
blank |
1 |
0 |
1 |
| 1 |
0 |
0 |
0 |
0 |
Descriptive Statements:
- Analyze relational and operational properties.
- Analyze a variety of conventional and alternative algorithms.
- Solve a variety of problems involving integers, fractions, and decimals.
- Solve a variety of problems involving ratios, proportions, and percents.
Sample Item:
A car that is advertised for $28,90028,900 dollars is sold after an 8% discount. If the commission rate is
0.75% of the sale price, how much money will the salesperson earn?
- $199.41199 dollars and 41 cents
- $216.75216 dollars and 75 cents
- $19,941.0019,941 dollars
- $21,675.0021,675 dollars
Correct Response and Explanation (Show Correct ResponseHide Correct Response)
A. This question requires the examinee to solve a variety of problems involving
ratios, proportions, and percents. The final sale price of the car is 92% of the asking price
(100% –to 8% discount) and the salesperson earns 0.75% of the sale price. Commission = ($28,900)(0.92)(0.0075) = $199.41Commission equals left parenthesis 28,900 dollars right parenthesis left parenthesis 0.92 cents right parenthesis left parenthesis 0.0075 cents right parenthesis equals 199 dollars and 41 cents.

